连续型特征归一化
- 数据的标准化(normalization)和归一化
数据的标准化(normalization)是将数据按比例缩放,使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到,去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或量级的指标能够进行比较和加权。其中最典型的就是数据的归一化处理,即将数据统一映射到[0,1]区间上。
目前数据标准化方法有多种,归结起来可以分为直线型方法(如极值法、标准差法)、折线型方法(如三折线法)、曲线型方法(如半正态性分布)。不同的标准化方法,对系统的评价结果会产生不同的影响,然而不幸的是,在数据标准化方法的选择上,还没有通用的法则可以遵循。 - 归一化的目标
1 把数变为(0,1)之间的小数
主要是为了数据处理方便提出来的,把数据映射到0~1范围之内处理,更加便捷快速,应该归到数字信号处理范畴之内。
2 把有量纲表达式变为无量纲表达式
归一化是一种简化计算的方式,即将有量纲的表达式,经过变换,化为无量纲的表达式,成为纯量。 比如,复数阻抗可以归一化书写:Z = R + jωL = R(1 + jωL/R) ,复数部分变成了纯数量了,没有量纲。
另外,微波之中也就是电路分析、信号系统、电磁波传输等,有很多运算都可以如此处理,既保证了运算的便捷,又能凸现出物理量的本质含义。 - 归一化后有两个好处
- 提升模型的收敛速度
如下图,x1的取值为0-2000,而x2的取值为1-5,假如只有这两个特征,对其进行优化时,会得到一个窄长的椭圆形,导致在梯度下降时,梯度的方向为垂直等高线的方向而走之字形路线,这样会使迭代很慢,相比之下,右图的迭代就会很快(理解:也就是步长走多走少方向总是对的,不会走偏)
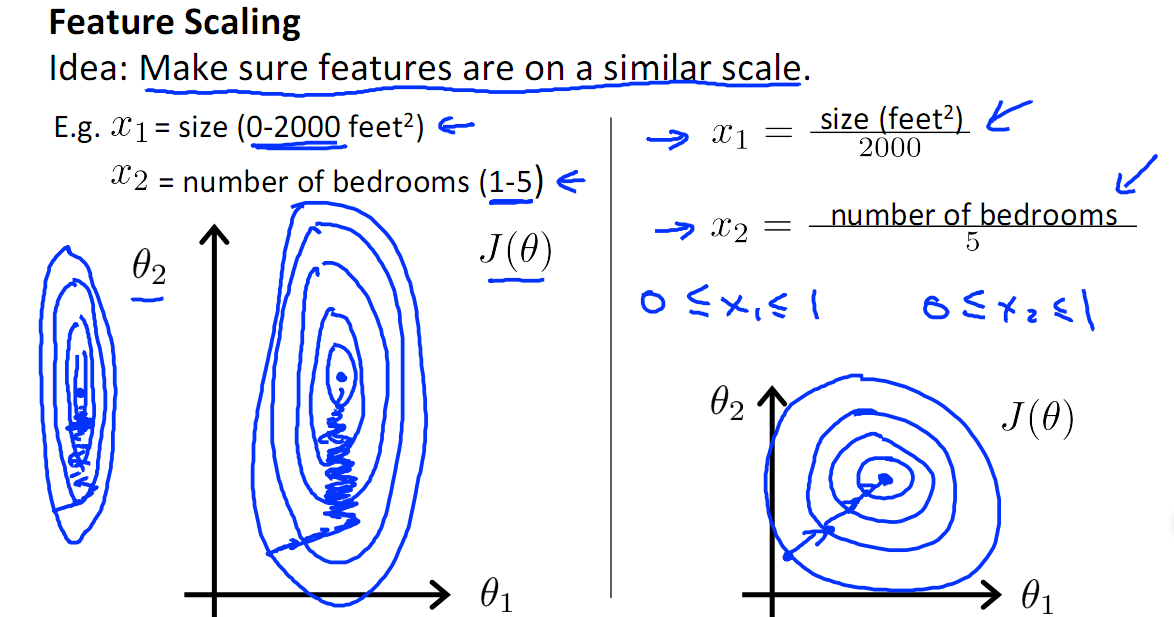
- 提升模型的精度
归一化的另一好处是提高精度,这在涉及到一些距离计算的算法时效果显著,比如算法要计算欧氏距离,上图中x2的取值范围比较小,涉及到距离计算时其对结果的影响远比x1带来的小,所以这就会造成精度的损失。所以归一化很有必要,他可以让各个特征对结果做出的贡献相同。
在多指标评价体系中,由于各评价指标的性质不同,通常具有不同的量纲和数量级。当各指标间的水平相差很大时,如果直接用原始指标值进行分析,就会突出数值较高的指标在综合分析中的作用,相对削弱数值水平较低指标的作用。因此,为了保证结果的可靠性,需要对原始指标数据进行标准化处理。
在数据分析之前,我们通常需要先将数据标准化(normalization),利用标准化后的数据进行数据分析。数据标准化也就是统计数据的指数化。数据标准化处理主要包括数据同趋化处理和无量纲化处理两个方面。数据同趋化处理主要解决不同性质数据问题,对不同性质指标直接加总不能正确反映不同作用力的综合结果,须先考虑改变逆指标数据性质,使所有指标对测评方案的作用力同趋化,再加总才能得出正确结果。数据无量纲化处理主要解决数据的可比性。经过上述标准化处理,原始数据均转换为无量纲化指标测评值,即各指标值都处于同一个数量级别上,可以进行综合测评分析。
从经验上说,归一化是让不同维度之间的特征在数值上有一定比较性,可以大大提高分类器的准确性。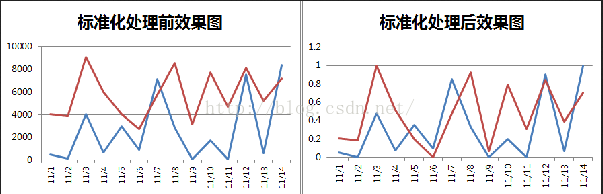
- 提升模型的收敛速度
- 数据需要归一化的机器学习算法
- 需要归一化的模型:
有些模型在各个维度进行不均匀伸缩后,最优解与原来不等价,例如SVM(距离分界面远的也拉近了,支持向量变多?)。对于这样的模型,除非本来各维数据的分布范围就比较接近,否则必须进行标准化,以免模型参数被分布范围较大或较小的数据dominate。
有些模型在各个维度进行不均匀伸缩后,最优解与原来等价,例如logistic regression(因为θ的大小本来就自学习出不同的feature的重要性吧?)。对于这样的模型,是否标准化理论上不会改变最优解。但是,由于实际求解往往使用迭代算法,如果目标函数的形状太“扁”,迭代算法可能收敛得很慢甚至不收敛。所以对于具有伸缩不变性的模型,最好也进行数据标准化。 - 不需要归一化的模型:
ICA好像不需要归一化(因为独立成分如果归一化了就不独立了?)。
基于平方损失的最小二乘法OLS不需要归一化。
- 需要归一化的模型:
常见的数据归一化方法
- min-max标准化(Min-max normalization)/0-1标准化(0-1 normalization)
也叫离差标准化,是对原始数据的线性变换,使结果落到[0,1]区间,转换函数如下:
其中max为样本数据的最大值,min为样本数据的最小值。def Normalization(x): return [(float(i)-min(x))/float(max(x)-min(x)) for i in x]如果想要将数据映射到[-1,1],则将公式换成:
x∗=x−xmeanxmax−xminx_mean表示数据的均值。
def Normalization2(x): return [(float(i)-np.mean(x))/(max(x)-min(x)) for i in x]这种方法有一个缺陷就是当有新数据加入时,可能导致max和min的变化,需要重新定义。
- log函数转换
通过以10为底的log函数转换的方法同样可以实现归一下,具体方法如下:
x=log10(x)/log10(max)
看了下网上很多介绍都是x=log10(x),其实是有问题的,这个结果并非一定落到[0,1]区间上,应该还要除以log10(max),max为样本数据最大值,并且所有的数据都要大于等于1。 - atan函数转换
用反正切函数也可以实现数据的归一化。
x=actn(x)2/π
使用这个方法需要注意的是如果想映射的区间为[0,1],则数据都应该大于等于0,小于0的数据将被映射到[-1,0]区间上,而并非所有数据标准化的结果都映射到[0,1]区间上。 - z-score 标准化(zero-mean normalization)
最常见的标准化方法就是Z标准化,也是SPSS中最为常用的标准化方法,spss默认的标准化方法就是z-score标准化。
也叫标准差标准化,这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。
经过处理的数据符合标准正态分布,即均值为0,标准差为1,其转化函数为:
x∗=x−μσ
其中μ为所有样本数据的均值,σ为所有样本数据的标准差。
z-score标准化方法适用于属性A的最大值和最小值未知的情况,或有超出取值范围的离群数据的情况。
标准化的公式很简单,步骤如下
1.求出各变量(指标)的算术平均值(数学期望)xi和标准差si ;
2.进行标准化处理:
zij=(xij-xi)/si
其中:zij为标准化后的变量值;xij为实际变量值。
3.将逆指标前的正负号对调。
标准化后的变量值围绕0上下波动,大于0说明高于平均水平,小于0说明低于平均水平。def z_score(x, axis): x = np.array(x).astype(float) xr = np.rollaxis(x, axis=axis) xr -= np.mean(x, axis=axis) xr /= np.std(x, axis=axis) # print(x) return x为什么z-score 标准化后的数据标准差为1?
x-μ只改变均值,标准差不变,所以均值变为0
(x-μ)/σ只会使标准差除以σ倍,所以标准差变为1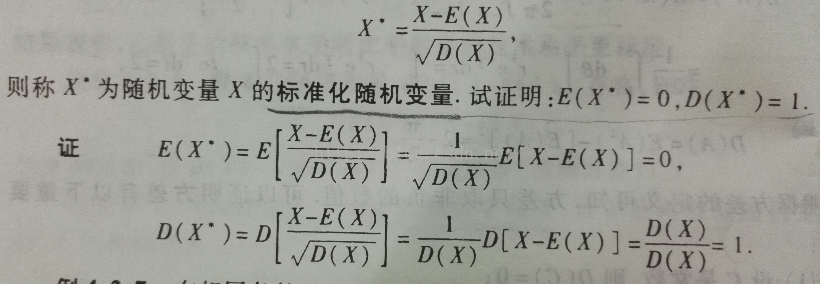
- Decimal scaling小数定标标准化
这种方法通过移动数据的小数点位置来进行标准化。小数点移动多少位取决于属性A的取值中的最大绝对值。
将属性A的原始值x使用decimal scaling标准化到x’的计算方法是:
x’=x/(10^j)
其中,j是满足条件的最小整数。
例如 假定A的值由-986到917,A的最大绝对值为986,为使用小数定标标准化,我们用每个值除以1000(即,j=3),这样,-986被规范化为-0.986。
注意,标准化会对原始数据做出改变,因此需要保存所使用的标准化方法的参数,以便对后续的数据进行统一的标准化。 -
Logistic/Softmax变换
logistic函数和标准正态函数
新数据=1/(1+e^(-原数据))
P(i)=11+exp(−θTix)
这个函数的作用就是使得P(i)在负无穷到0的区间趋向于0,在0到正无穷的区间趋向于1。同样,函数(包括下面的softmax)加入了e的幂函数正是为了两极化:正样本的结果将趋近于1,而负样本的结果趋近于0。这样为多类别分类提供了方便(可以把P(i)看作是样本属于类别i的概率)。
logit(P) = log(P / (1-P)) = a + bx 以及 probit(P) = a + bx
这两个连接函数的性质使得P的取值被放大到整个实数轴上。
事实上可以把上面的公式改写一下:
P = exp(a + bx) / (1 + exp(a + bx)) 或者 P = pnorm(a + b*x)(这个是标准正态分布的分布函数)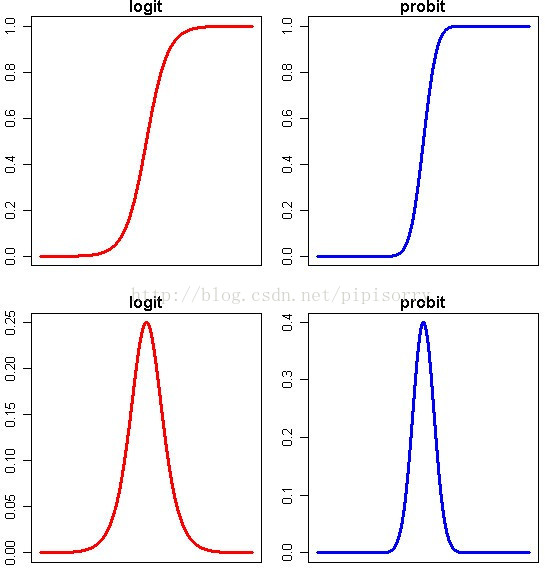
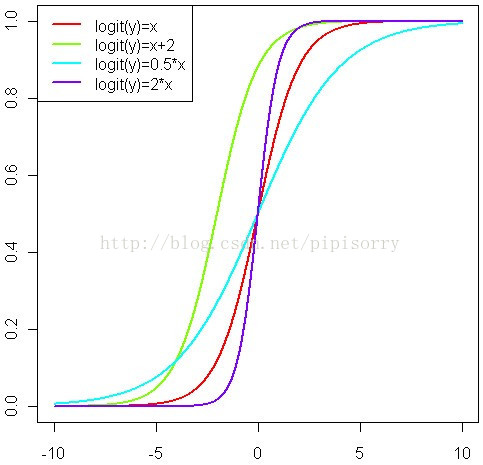 Note: 上半部分图形显示了概率P随着自变量变化而变化的情况,下半部分图形显示了这种变化的速度的变化。可以看得出来,概率P与自变量仍然存在或多或少的线性关系,主要是在头尾两端被连接函数扭曲了,从而实现了[0,1]限制。同时,自变量取值靠近中间的时候,概率P变化比较快,自变量取值靠近两端的时候,概率P基本不再变化。这就跟我们的直观理解相符合了,似乎是某种边际效用递减的特点。
Note: 上半部分图形显示了概率P随着自变量变化而变化的情况,下半部分图形显示了这种变化的速度的变化。可以看得出来,概率P与自变量仍然存在或多或少的线性关系,主要是在头尾两端被连接函数扭曲了,从而实现了[0,1]限制。同时,自变量取值靠近中间的时候,概率P变化比较快,自变量取值靠近两端的时候,概率P基本不再变化。这就跟我们的直观理解相符合了,似乎是某种边际效用递减的特点。 -
Softmax函数 是logistic函数的一种泛化,Softmax是一种形如下式的函数:
假设我们有一个数组,V,Vi表示V中的第i个元素,那么这个元素的Softmax值就是
也就是说,是该元素的指数,与所有元素指数和的比值
为什么要取指数,第一个原因是要模拟 max 的行为,所以要让大的更大。第二个原因是需要一个可导的函数。
通过softmax函数,可以使得P(i)的范围在[0,1]之间。在回归和分类问题中,通常θ是待求参数,通过寻找使得P(i)最大的θi作为最佳参数。
此外Softmax函数同样可用于非线性估计,此时参数θ可根据现实意义使用其他列向量替代。
Softmax函数得到的是一个[0,1]之间的值,且∑Kk=1P(i)=1,这个softmax求出的概率就是真正的概率,换句话说,这个概率等于期望。 - 模糊量化模式 新数据=1/2+1/2sin[派3.1415/(极大值-极小值)*(X-(极大值-极小值)/2) ] X为原数据
离散型特征归一化(独热编码(One-Hot Encoding))
在很多机器学习任务中,特征并不总是连续值,而有可能是分类值.
例如,考虑一下的三个特征:
["male", "female"]
["from Europe", "from US", "from Asia"]
["uses Firefox", "uses Chrome", "uses Safari", "uses Internet Explorer"]
如果将上述特征用数字表示,效率会高很多.例如:
["male", "from US", "uses Internet Explorer"] 表示为[0, 1, 3]
["female", "from Asia", "uses Chrome"]表示为[1, 2, 1]
但是,即使转化为数字表示后,上述数据也不能直接用在我们的分类器中.因为,分类器往往默认数据数据是连续的(可以计算距离?),并且是有序的(而上面这个0并不是说比1要高级).但是,按照我们上述的表示,数字并不是有序的,而是随机分配的.
- 独热编码
为了解决上述问题,其中一种可能的解决方法是采用独热编码(One-Hot Encoding).独热编码即 One-Hot 编码,又称一位有效编码,其方法是使用N位状态寄存器来对N个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候,其中只有一位有效.
例如:
自然状态码为:000,001,010,011,100,101
独热编码为:000001,000010,000100,001000,010000,100000
可以这样理解,对于每一个特征,如果它有m个可能值,那么经过独热编码后,就变成了m个二元特征(如成绩这个特征有好,中,差变成one-hot就是100, 010, 001).并且,这些特征互斥,每次只有一个激活.因此,数据会变成稀疏的.
这样做的好处主要有:
解决了分类器不好处理属性数据的问题
在一定程度上也起到了扩充特征的作用
举例
基于Scikit-learn的例子:from sklearn import preprocessing enc = preprocessing.OneHotEncoder() enc.fit([[0, 0, 3], [1, 1, 0], [0, 2, 1], [1, 0, 2]]) enc.transform([[0, 1, 3]]).toarray()输出结果:
array([[ 1., 0., 0., 1., 0., 0., 0., 0., 1.]])Note: fit了4个数据3个特征,而transform了1个数据3个特征.第一个特征两种值(0: 10, 1: 01),第二个特征三种值(0: 100, 1: 010, 2: 001),第三个特征四种值(0: 1000, 1: 0100, 2: 0010, 3: 0001).所以转换[0, 1, 3]为[ 1., 0., 0., 1., 0., 0., 0., 0., 1.].
处理离散型特征和连续型特征并存的情况
- 离散型特征的处理方法:
a) Binarize categorical/discrete features: For all categorical features, represent them as multiple boolean features. For example, instead of having one feature called marriage_status, have 3 boolean features - married_status_single, married_status_married, married_status_divorced and appropriately set these features to 1 or -1. As you can see, for every categorical feature, you are adding k binary feature where k is the number of values that the categorical feature takes.对于离散的特征基本就是按照one-hot编码,该离散特征有多少取值,就用多少维来表示该特征。
为什么使用one-hot编码来处理离散型特征?
1、Why do we binarize categorical features?
We binarize the categorical input so that they can be thought of as a vector from the Euclidean space (we call this as embedding the vector in the Euclidean space).使用one-hot编码,将离散特征的取值扩展到了欧式空间,离散特征的某个取值就对应欧式空间的某个点。
2、Why do we embed the feature vectors in the Euclidean space?
Because many algorithms for classification/regression/clustering etc. requires computing distances between features or similarities between features. And many definitions of distances and similarities are defined over features in Euclidean space. So, we would like our features to lie in the Euclidean space as well.将离散特征通过one-hot编码映射到欧式空间,是因为,在回归,分类,聚类等机器学习算法中,特征之间距离的计算或相似度的计算是非常重要的,而我们常用的距离或相似度的计算都是在欧式空间的相似度计算,计算余弦相似性,基于的就是欧式空间。
3、Why does embedding the feature vector in Euclidean space require us to binarize categorical features?
Let us take an example of a dataset with just one feature (say job_type as per your example) and let us say it takes three values 1,2,3.
Now, let us take three feature vectors x_1 = (1), x_2 = (2), x_3 = (3). What is the euclidean distance between x_1 and x_2, x_2 and x_3 & x_1 and x_3? d(x_1, x_2) = 1, d(x_2, x_3) = 1, d(x_1, x_3) = 2. This shows that distance between job type 1 and job type 2 is smaller than job type 1 and job type 3. Does this make sense? Can we even rationally define a proper distance between different job types? In many cases of categorical features, we can properly define distance between different values that the categorical feature takes. In such cases, isn’t it fair to assume that all categorical features are equally far away from each other?
Now, let us see what happens when we binary the same feature vectors. Then, x_1 = (1, 0, 0), x_2 = (0, 1, 0), x_3 = (0, 0, 1). Now, what are the distances between them? They are sqrt(2). So, essentially, when we binarize the input, we implicitly state that all values of the categorical features are equally away from each other.
将离散型特征使用one-hot编码,确实会让特征之间的距离计算更加合理。比如,有一个离散型特征,代表工作类型,该离散型特征,共有三个取值,不使用one-hot编码,其表示分别是x_1 = (1), x_2 = (2), x_3 = (3)。两个工作之间的距离是,(x_1, x_2) = 1, d(x_2, x_3) = 1, d(x_1, x_3) = 2。那么x_1和x_3工作之间就越不相似吗?显然这样的表示,计算出来的特征的距离是不合理。那如果使用one-hot编码,则得到x_1 = (1, 0, 0), x_2 = (0, 1, 0), x_3 = (0, 0, 1),那么两个工作之间的距离就都是sqrt(2).即每两个工作之间的距离是一样的,显得更合理。
4、About the original question?
Note that our reason for why binarize the categorical features is independent of the number of the values the categorical features take, so yes, even if the categorical feature takes 1000 values, we still would prefer to do binarization.
5、Are there cases when we can avoid doing binarization?没必要用one-hot 编码的情形Yes. As we figured out earlier, the reason we binarize is because we want some meaningful distance relationship between the different values. As long as there is some meaningful distance relationship, we can avoid binarizing the categorical feature. For example, if you are building a classifier to classify a webpage as important entity page (a page important to a particular entity) or not and let us say that you have the rank of the webpage in the search result for that entity as a feature, then 1] note that the rank feature is categorical, 2] rank 1 and rank 2 are clearly closer to each other than rank 1 and rank 3, so the rank feature defines a meaningful distance relationship and so, in this case, we don’t have to binarize the categorical rank feature.
More generally, if you can cluster the categorical values into disjoint subsets such that the subsets have meaningful distance relationship amongst them, then you don’t have binarize fully, instead you can split them only over these clusters. For example, if there is a categorical feature with 1000 values, but you can split these 1000 values into 2 groups of 400 and 600 (say) and within each group, the values have meaningful distance relationship, then instead of fully binarizing, you can just add 2 features, one for each cluster and that should be fine.
将离散型特征进行one-hot编码的作用,是为了让距离计算更合理,但如果特征是离散的,并且不用one-hot编码就可以很合理的计算出距离,那么就没必要进行one-hot编码,比如,该离散特征共有1000个取值,我们分成两组,分别是400和600,两个小组之间的距离有合适的定义,组内的距离也有合适的定义,那就没必要用one-hot 编码。
离散特征进行one-hot编码后,编码后的特征,其实每一维度的特征都可以看做是连续的特征。就可以跟对连续型特征的归一化方法一样,对每一维特征进行归一化。比如归一化到[-1,1]或归一化到均值为0,方差为1。
有些情况不需要进行特征的归一化:
It depends on your ML algorithms, some methods requires almost no efforts to normalize features or handle both continuous and discrete features, like tree based methods: c4.5, Cart, random Forrest, bagging or boosting. But most of parametric models (generalized linear models, neural network, SVM,etc) or methods using distance metrics (KNN, kernels, etc) will require careful work to achieve good results. Standard approaches including binary all features, 0 mean unit variance all continuous features, etc。
基于树的方法是不需要进行特征的归一化,例如随机森林,bagging 和 boosting等。基于参数的模型或基于距离的模型,都是要进行特征的归一化。
one-hot编码为什么可以解决类别型数据的离散值问题
首先,one-hot编码是N位状态寄存器为N个状态进行编码的方式
eg:高、中、低不可分,→ 用0 0 0 三位编码之后变得可分了,并且成为互相独立的事件
→ 类似 SVM中,原本线性不可分的特征,经过project之后到高维之后变得可分了
GBDT处理高维稀疏矩阵的时候效果并不好,即使是低维的稀疏矩阵也未必比SVM好
- Tree Model不太需要one-hot编码
对于决策树来说,one-hot的本质是增加树的深度
tree-model是在动态的过程中生成类似 One-Hot + Feature Crossing 的机制- 一个特征或者多个特征最终转换成一个叶子节点作为编码 ,one-hot可以理解成三个独立事件
- 决策树是没有特征大小的概念的,只有特征处于他分布的哪一部分的概念
one-hot可以解决线性可分问题 但是比不上label econding
one-hot降维后的缺点:
降维前可以交叉的降维后可能变得不能交叉
树模型的训练过程:
从根节点到叶子节点整条路中有多少个节点相当于交叉了多少次,所以树的模型是自行交叉
eg:是否是长的 { 否(是→ 柚子,否 → 苹果) ,是 → 香蕉 } 园 cross 黄 → 形状 (圆,长) 颜色 (黄,红) one-hot度为4的样本
使用树模型的叶子节点作为特征集交叉结果可以减少不必要的特征交叉的操作 或者减少维度和degree候选集
eg 2 degree → 8的特征向量 树 → 3个叶子节点
树模型:Ont-Hot + 高degree笛卡尔积 + lasso 要消耗更少的计算量和计算资源
这就是为什么树模型之后可以stack线性模型
nm的输入样本 → 决策树训练之后可以知道在哪一个叶子节点上 → 输出叶子节点的index → 变成一个n1的矩阵 → one-hot编码 → 可以得到一个n*o的矩阵(o是叶子节点的个数) → 训练一个线性模型
典型的使用: GBDT + RF
优点 : 节省做特征交叉的时间和空间
如果只使用one-hot训练模型,特征之间是独立的
对于现有模型的理解:(G(l(张量))):
其中:l(·)为节点的模型
G(·)为节点的拓扑方式
神经网络:l(·)取逻辑回归模型
G(·)取全连接的方式
决策树: l(·)取LR
G(·)取树形链接方式
创新点: l(·)取 NB,SVM 单层NN ,等
G(·)取怎样的信息传递方式
onehot编码实现
onehot = (np.arange(num_labels) == labels[:, None]).astype(np.float32)
from sklearn import preprocessing
enc = preprocessing.OneHotEncoder(sparse=False)
onehot = enc.fit_transform(nominal.values)
转自:http://blog.csdn.net/pipisorry/article/details/52247379